Mechanics of the World, Pt. 2


American Disclaimer: This post makes extensive use of SI units.
To start, I changed those arbitrary elevation units to kilometers. It came with some troubles and bugs, but nothing too hard. And now the planet radius is changeable! By default it's now 5000km, or about 1500km less than the Earth's radius. But switching to kilometers was nothing compared to what was coming next.
Fourier, Fourier, Fourier..
A few of you might be familiar with what's called the Fourier law, it's the base equation for computing thermal conduction, which is simply physicists way to say that when an hot object touches a cold object, the heat transfers from one to the other. It's the reason putting ice in your drink cools it (alongside convection, which is a whole another topic for next time I guess).
According to Wikipedia:
> The law of heat conduction, also known as Fourier's law, states that the rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat flows.
Understood? Ok great. More seriously, what it means is that according to Fourier's law, the higher the temperature difference (gradient) is between the two bodies, the more heat is transferred. The reason why the gradient is negative is because heat always transfer from the hot point to the cold point. Taking our drink example, what actually happens is that your drink transfers heat to the ice: hence the ice block heats and may eventually melt, and the drink cools because it lost heat energy.
Now the thing is, computing a 3D temperature gradient (temperature difference) is hard, like really hard, when the points are in a sphere and not organized like in cubes. But just by looking outside the box, you can notice we only need to compute a 1D gradient as we're only looking at two points at once. And turns out that in 1D, a gradient is literally just a difference. So just a substraction.
So we take our equation
q = -k∇T
where q is in W/m², k is the conductivity, and ∇T is our famous temperature gradient. And because we're only looking in 1D, we can turn this equation into this new one:
q = -k * ΔT/Δx
where ΔT is the difference in temperature of the points, and Δx the distance between the two points.
And that's it, this way we get our heat transfer, wait no. It's heat flux density.. and it's in W/m².....
Fortunately, we can convert that to Kelvin / Celsius temperature using dimensional analysis, aka more M.A.T.H.
(note:
Δt is the time elapsed between the last simulation tick and the current one
heat capacity is in J/K)
q = -k * ΔT/Δx # This value is in W/m² power = q * area # We multiply by the area covered by a point to get W (Watt) heat transfer = q * Δt # W = J/s, so to get J (Joules) we multiply by the time. temperature gain = heat transfer / heat capacity # J / (J / K) is equivalent to K (Kelvin)
And we got the transferred temperature, measured in Kelvin!
Next up are solar irradiance and black-body thermal radiation (Stefan-Boltzmann law) that are similarly implemented.
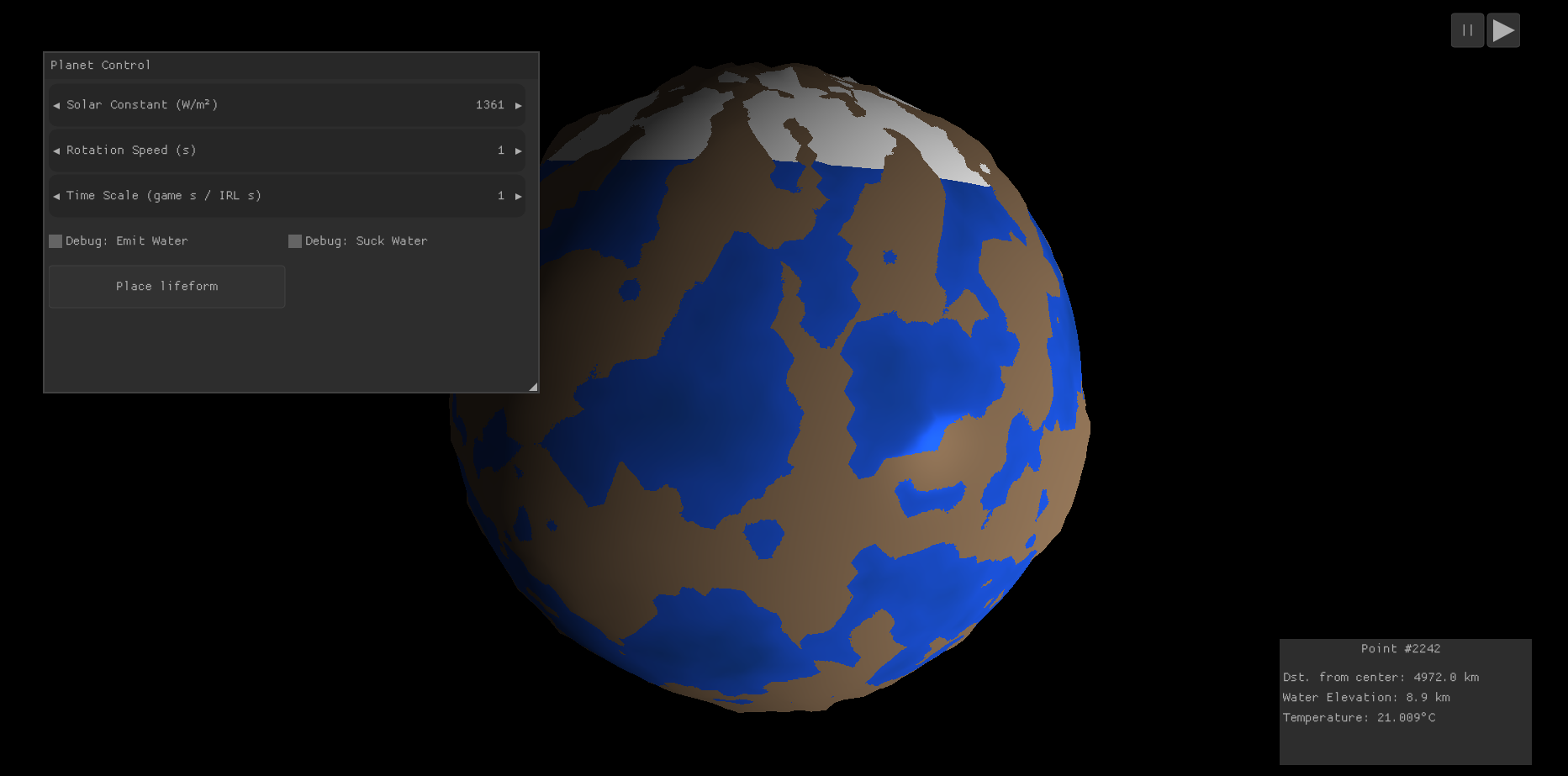
In the end, surface conductivity slider disappeared (for good reasons, let's avoid bending laws of physics more than they already are) and axial tilt disappeared too but I plan to add it back later.
More features
I also switched to 3D perlin noise which meant better terrain quality which is really visible at the poles (compare to the above image), I added normals which meant lighting now feels better, and I exaggerated altitude by a factor of 10. So 3km above sea level now appears as 30km above sea level, because otherwise it looks really flat. And finally, I switched the ico-sphere to 7 steps (41000 points on one sphere!)

Starting to look like it does today? That's because it was 2 months ago and I haven't changed much in graphics since then. I then spent a month working on rabbits life that wouldn't fly out to outer space (they must be preparing Plan 9).

And then another month was spent on optimization (making the code run faster). Because remember kids, optimization is hard but necessary otherwise you get games that need an RTX 3080 to render a single rock. I then tried to switch water simulation to a Navier-Stokes solver, but I post-poned this one.. which means a problem for future me! Yay!
To finish off, here's what the game would look with an ico-sphere at 9 steps (so that's what that Plan 9 was all about!) which makes the game lags so much that simulation runs like a slideshow but atleast it doesn't crash thanks to optimization.

You can play the game for free!
Files
Get Stella Dei
Stella Dei
Customize your planet in this SimEarth-inspired game
| Status | In development |
| Author | zenith391 |
| Genre | Simulation |
| Tags | 3D, evolution, god-game, planet, Sandbox, Singleplayer, Space |
| Languages | English |
More posts
- Stella Dei 0.2.0Feb 18, 2023
- Stella Dei 0.1.1Jun 28, 2022
- Mechanics of the World, Pt. 1Jun 11, 2022

Leave a comment
Log in with itch.io to leave a comment.